Thermal mass

What is thermal mass?

In simple terms, thermal mass is the ability of a material to absorb, store and release heat. Materials such as concrete, bricks and tiles absorb and store heat. They are therefore said to have high thermal mass. Materials such as timber and cloth do not absorb and store heat and are said to have low thermal mass.

In considering thermal mass, you will also need to consider thermal lag. Thermal lag is the rate at which heat is absorbed and released by a material. Materials with long thermal lag times (for example, brick and concrete) will absorb and release heat slowly; materials with short thermal lag times (for example, steel) will absorb and release heat quickly.

Photo: Amber Creative

Thermal mass

Thermal mass, or the ability to store heat, is also known as volumetric heat capacity (VHC). VHC is calculated by multiplying the specific heat capacity by the density of a material: 

• Specific heat capacity is the amount of energy required to raise the temperature of 1kg of a material by 1°C.
• Density is the weight per unit volume of a material (ie how much a cubic metre the material weighs). 

The higher the VHC, the higher the thermal mass.



Water has the highest VHC of any common material. The following table shows that it takes 4186 kilojoules (kJ) of energy to raise the temperature of 1 cubic metre of water by 1°C, whereas it takes only 2060kJ to raise the temperature of an equal volume of concrete by the same amount. In other words, water has around twice the heat storage capacity of concrete. The VHC of rock usually ranges between brick and concrete, depending on density. Most common building materials with high VHC also tend to be quite conductive, making them poor insulators. 

Thermal mass of various materials

Source: Baggs and Mortensen 2006

Thermal lag

How fast heat is absorbed and released by uninsulated material is referred to as thermal lag. It is influenced by:

• heat capacity of the material
• conductivity of the material
• difference in temperature (known as the temperature differential or ΔT) between each face of the material
• thickness of the material
• surface area of the material
• texture, colour and surface coatings (for example, dark, matte or textured surfaces absorb and re-radiate more energy than light, smooth, reflective surfaces)
• exposure of the material to air movement and air speed.

To be effective in most climates, thermal mass should be able to absorb and re-radiate close to its full heat storage capacity in a single day–night (diurnal) cycle.

In moderate climates, a 12-hour lag cycle is ideal. In colder climates subject to long cloudy periods, lags of up to 7 days can be useful, providing there is enough solar exposed glazing to ‘charge’ the thermal mass in sunny weather.

Embodied energy

Some high thermal mass materials, such as concrete, cement-stabilised rammed earth, and brick, have high embodied energy when used in the quantities required. This highlights the importance of using such construction only where it delivers a clear thermal benefit. When used appropriately, the savings in heating and cooling energy from the thermal mass can outweigh the cost of its embodied energy over the lifetime of the building. Consideration should be given to using high thermal mass materials with lower embodied energy, such as water, adobe or recycled brick. 

Why is thermal mass important?

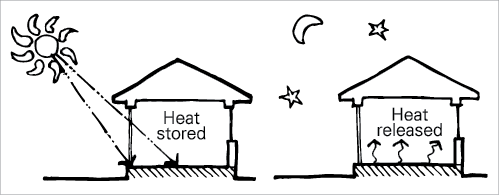
When used correctly, materials with high thermal mass can significantly increase comfort and reduce energy use in your home. Thermal mass acts as a thermal battery to moderate internal temperatures by averaging out day−night (diurnal) extremes.



In winter, thermal mass can absorb heat during the day from direct sunlight. It re-radiates this warmth back into the home throughout the night. 

 

In summer, thermal mass can be used to keep the home cool. If the sun is blocked from reaching the mass (for example, with shading), the mass will instead absorb warmth from inside the home. You can then allow cool breezes and convection currents to pass over the thermal mass overnight to draw out the stored energy. 



Conversely, poor use of thermal mass can reduce comfort and increase energy use. Inappropriate thermal mass can absorb all the heat you produce on a winter night or radiate heat to you all night as you try to sleep during a summer heatwave. 

 

To be effective, thermal mass must be integrated with sound passive design techniques.



The amount of heat absorbed by thermal mass is heavily influenced by glazing areas, glazing type and shading. The greater the need for heat, the larger area of high-solar-transmission glass required. Conversely, the reverse is true in hotter climates. 



Insulation levels and air tightness will also influence how long the captured heat is held within the home. 



Mass levels should vary according to:

• your climate zone 
• solar access (window and glazing type, orientation and shading)
• insulation levels
• air tightness
• cool breeze and night air access 
• diffuse heat gains in summer
• occupation patterns
• heating and cooling system use.

Thermal mass is usually a consideration when buying or building a home, but some changes can be retrofitted (for example, exposing concrete slabs, adding interior masonry walls or water-filled containers).

General principles for locating thermal mass

Some general principles can be followed for where to locate – and not locate – thermal mass.

Where to locate thermal mass

To determine the best location for thermal mass, identify whether your house requires passive heating, passive cooling, or both.

• For passive heating, locate thermal mass in areas that receive direct sunlight or radiant heat from heaters.
• For passive cooling, protect thermal mass from summer sun with shading and insulation. Ensure cool night breezes and air currents can pass over the thermal mass to draw out stored energy. 
• For both passive heating and cooling, locate thermal mass inside the building on the ground floor for ideal summer and winter efficiency. Locate thermal mass in north-facing rooms with good solar access, exposure to cooling night breezes in summer, and additional sources of heating or cooling. Include appropriate shading to protect the mass from summer sun.
• Locate additional thermal mass near the centre of the building, particularly if an air-conditioner is positioned there. Feature brick walls, slabs, water features and large earth or water-filled pots or even water tanks can be used.

Where not to locate thermal mass

Avoid thermal mass in rooms and buildings with poor insulation from external temperature extremes and rooms with minimal exposure to winter sun or cooling summer breezes.



Thermal mass may decrease comfort when used in rooms where heating or cooling is required but used intermittently, because it slows the response times. 



Careful design is required if locating thermal mass on the upper levels of multistorey housing in all but cold climates, especially if these are bedroom areas. Natural convection creates higher temperatures in upstairs rooms and upper level thermal mass absorbs this energy. On hot nights, upper level thermal mass can be slow to cool, causing discomfort while sleeping. 

Climate-specific designs

For thermal mass to be effective, it must suit the climate. It is possible to design a high thermal mass building for almost any climate but more extreme climates require careful design.



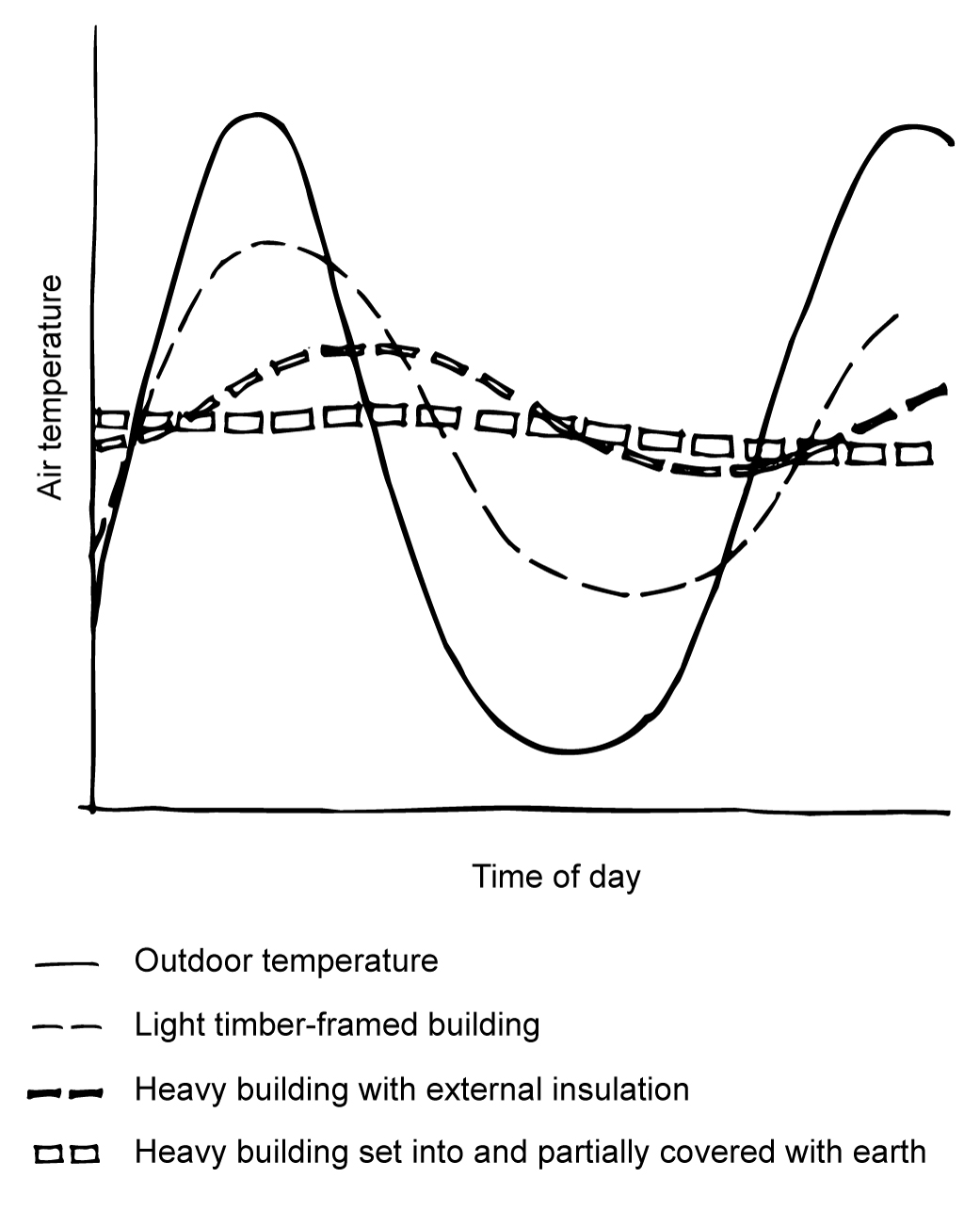
Thermal mass is most appropriate in climates with a larger diurnal temperature range – the difference between day and night outdoor temperatures. The average diurnal range is a useful indicator of appropriate thermal mass levels in a house:

• Low-mass construction (for example, lightweight timber-framed construction) generally performs best where diurnal ranges are consistently 6°C or less (coastal, hot humid and temperate climates). In tropical climates with diurnal ranges of 7°C−8°C (for example, Cairns), high-mass construction can cause overheating unless carefully designed, well shaded, and insulated.
• Moderate mass (for example, slab-on-ground, lightweight insulated walls such as brick veneer) is best for a 6°−10°C diurnal range.
• High-mass construction (that is, slab-on-ground and high mass walls) is desirable for a diurnal range over 10°C. 

In cool or cold climates where supplementary heating is often used, houses can benefit from high-mass construction regardless of diurnal range even where solar access is suboptimal. A home with high mass, high insulation and airtight construction will hold a comfortable temperature overnight if heated during the day. 

House energy rating software can model your specific house design and climate zone to test effective strategies. It is recommended that owners and builders use a Nationwide House Energy Rating Scheme (NatHERS) accredited assessor to determine a home’s energy rating.

Hot humid climates (Climate zones 1 and 2)

Use of high-mass construction is generally not recommended in hot humid climates because they have limited diurnal range and relatively high night-time temperatures. Passive cooling in this climate is usually more effective in low-mass buildings.



Thermal comfort during sleeping hours is a primary design consideration in tropical climates. Lightweight construction responds quickly to cooling breezes. High mass, if not properly designed and managed, can completely negate these benefits by slowly releasing heat at night that was absorbed during the day.



If you have access to solar energy, you can boost the performance of your thermal mass by using air-conditioning to cool the mass during the day without cost or emissions. This strategy is most effective in an airtight building.

Hot dry climates (Climate zones 3 and 4)

Both winter heating and summer cooling are very important in these climates. High-mass construction, combined with sound passive heating and cooling principles, is the most effective and economical means of maintaining thermal comfort.



Day–night (diurnal) temperature ranges are generally quite significant and can be extreme. High-mass construction with high insulation and airtightness levels is ideal in these conditions.

 

Where supplementary heating or cooling is provided, locate thermal mass nearby. The mass will moderate temperature variations and reduce the duration of auxiliary requirements while increasing thermal comfort. With the low humidity in these climates, ceiling fans generally provide adequate cooling comfort in a well-designed home.

Earth-covered homes give protection from solar radiation and provide additional thermal mass through earth coupling to stabilise internal air temperatures. Adequate solar access to windows is needed to achieve winter comfort levels. Alternatively, a solar PV-powered heating system can be used to keep your house warm without added electricity costs or emissions.

Warm and mild temperate climates (Climate zones 5 and 6)

Maintaining thermal comfort in these climates is relatively easy. Well-designed houses should require minimal supplementary heating or cooling, and 7.5−8 NatHERS stars can be achieved without high costs through good design.



The predominant requirement for cooling in these climates is often suited to lightweight, low-mass construction. High-mass construction is also appropriate, but requires sound passive design to avoid overheating in summer.



In multilevel design, high-mass construction should ideally be used on lower levels to stabilise temperatures. Low mass on the upper levels ensures that, as hot air rises, the heat is not stored in the upper level.



This is particularly important if sleeping spaces are located on upper levels. Ground- and first-floor spaces should be able to be closed off to prevent temperature stratification in winter. 

Photo: © Finn Howard Photography

Cool temperate and alpine climates (Climate zones 7 and 8)

Winter heating is the main need in these climates, although some summer cooling is generally required. Ceiling fans usually provide adequate comfort in these low-humidity climates.



High-mass construction combined with sound passive solar design and high levels of insulation and airtightness is an ideal solution. Good solar access is required in winter to heat the thermal mass. Appropriate glass-to-mass ratios are critical; these are best determined through thermal modelling.



Slab edges should always be insulated in these climates. It is also advisable to insulate the underside of a slab-on-ground in these climates as the reduction in heating demand tends to be greater than the reduction in summer cooling demand.



Buildings that receive little or no passive solar gains can still benefit from high-mass construction if they are well insulated and airtight. However, they respond slowly to heating input and are best kept at consistent temperatures using efficient systems.

Types of thermal mass

Concrete slabs

Concrete slabs can be either constructed on-ground or suspended above ground. Suspended slabs should always be insulated.

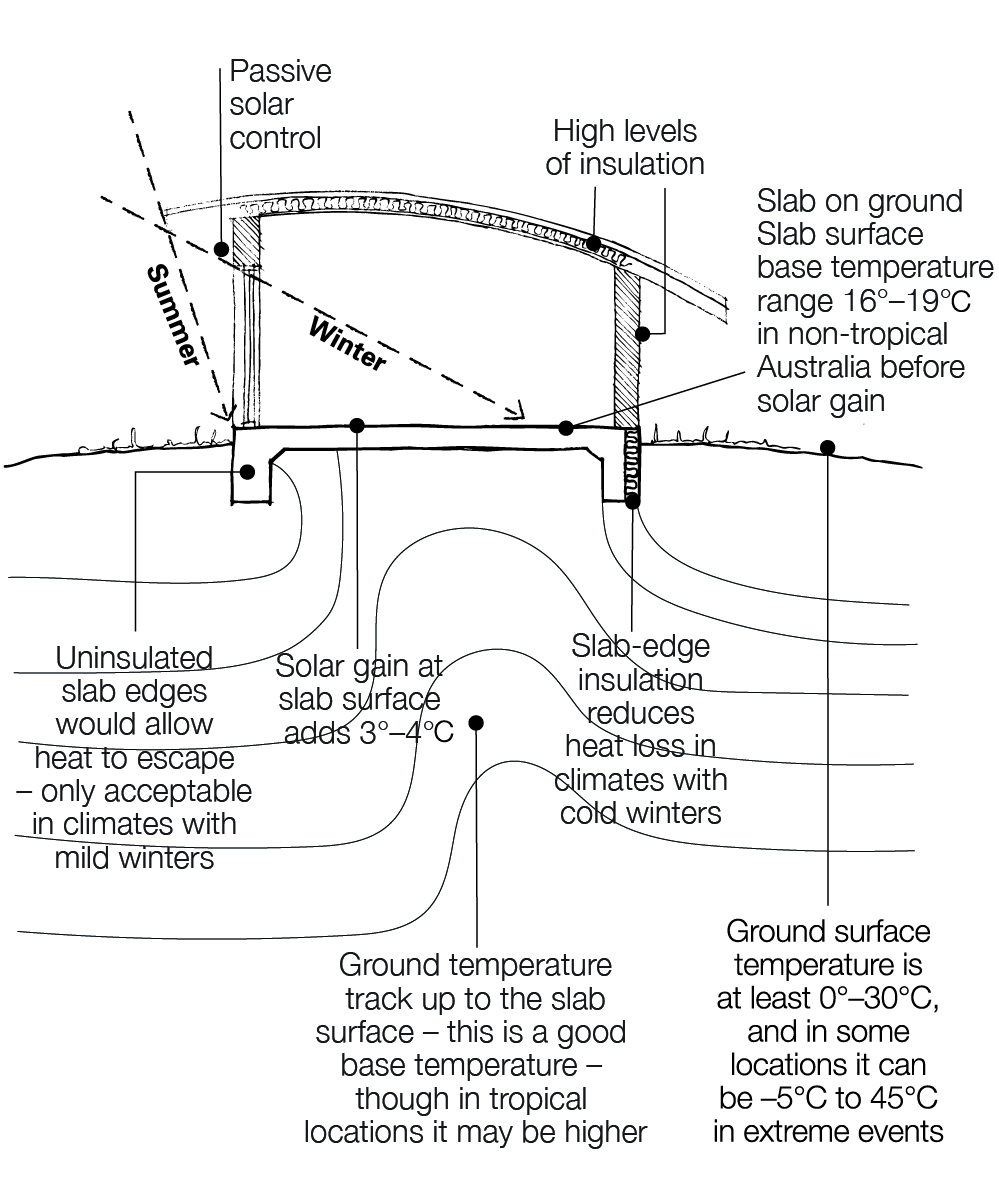
In some climates it is useful to connect the thermal mass in floors to the earth. The most common example is slab-on-ground construction. Less common examples are brick or earthen floors or earth-covered homes.

This is known as earth coupling. The earth acts as an insulator to reduce heat loss from the slab and connects the house to deeper ground temperatures, which are more stable.

In summer, where floor surfaces have a continuous thermal connection with the earth (like tiles or polished concrete), it can ‘wick’ away substantial heat loads. It also provides a cooler surface for occupants’ bodies to radiate heat to (or conduct to, with bare feet). This increases both psychological and physiological comfort.

In winter, a ground-connected slab can maintain a higher temperature than a slab to ambient air (for example, a suspended slab). The addition of passive solar or mechanical heating is then more effective due to the lower temperature increase required to achieve comfortable temperatures than if the slab were exposed to outdoor air.

Slab design

Use surfaces such as quarry or ceramic tiles or polished concrete slab. To maximise heating and cooling potential of your thermal mass floors, minimise carpets and rugs and do not cover areas of the slab exposed to winter sun with carpet, cork, wood or other insulating materials: use rugs if you wish, but in areas out of the sun.

Slab insulation

In climates where the ground temperatures are below comfort levels in winter, it is beneficial to insulate under a slab to reduce heat loss to the ground over the winter months. In hot climates, under-slab insulation can prevent a constant source of heat entering the home.

Depending on the climate, the summer cooling benefit of earth coupling (reduction in energy demand) may or may not exceed the additional energy required in winter to compensate for the uninsulated slab on ground. It is important to get the balance correct by raising these issues with your designer and energy advisor.

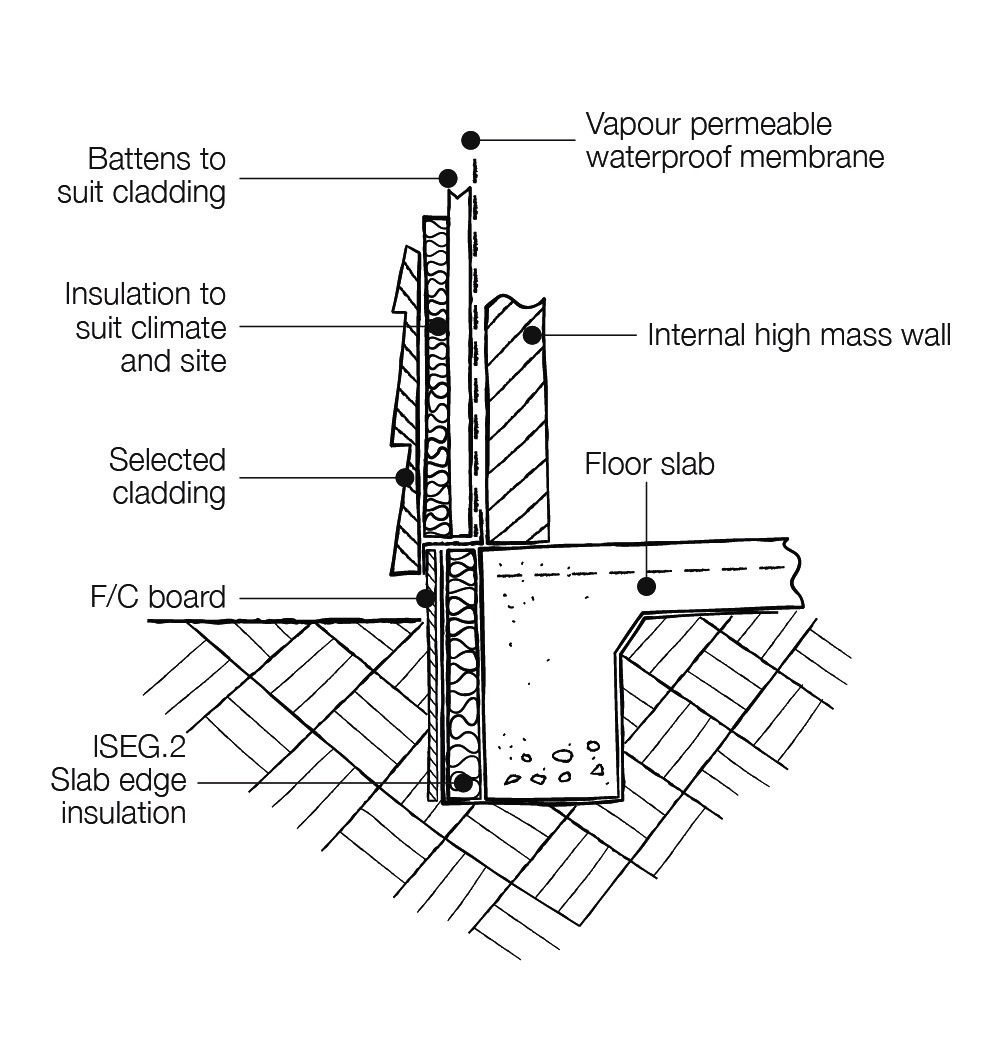
Insulating the slab edge is a good idea, as it protects the slab edges from being heated or cooled by the changes in shallow soil temperatures adjacent to it. Uninsulated vertical slab edges conduct energy through the building envelope. Condensation may occur in climates where the outdoor winter night temperatures are low.

The National Construction Code (NCC) requires vertical edges of a slab-on-ground to be insulated in Climate zone 8 (cold climate) or when in-slab heating or cooling is installed within the slab.

Consider termite proofing when designing slab edge insulation. Take care to ensure that the type of termite management system selected is compatible with the slab edge insulation.

Walls

Masonry walls provide good thermal mass if they are located internally or protected by insulation. Avoid finishing masonry walls with plasterboard because this insulates the thermal mass from the interior and reduces its capacity to absorb and release heat. 



Reverse brick veneer construction is an example of good thermal mass practice for external walls because the mass is on the inside and externally insulated. In traditional brick veneer, the mass of the brick makes no contribution to thermal storage because it is insulated from the inside and not the outside. Double-cavity brickwork can also provide good thermal mass if the cavity is appropriately insulated.

 

Water

Water-filled containers can be used as a mass substitute. Water has double the thermal storage capacity of concrete and heat absorption is substantially higher because of convection within the container. Water can supply similar storage capacity to masonry with significantly less mass and bulk, making water a cost-effective mass option for upper storeys.



However, caution should be taken using water inside a building. Enclosed containers with the addition of a small amount of chemical to control algae growth are considered best practice for water being used as thermal mass.



Internal or enclosed water features such as pools can also provide thermal mass, but require good ventilation. They should also be able to be isolated, because evaporation can absorb heat in winter and create condensation problems year round.

 

Photo: Petri Kurkaa

Phase-change materials

There is growing interest in the use of phase-change materials (PCMs) as a lightweight thermal mass substitute in construction. 

All materials require energy input to change state (that is, from a solid to a liquid or a liquid to a gas). This energy does not change their temperature, only their state. All materials change state at different temperatures (for example, water changes state to ice at 0°C).

With PCMs that are aligned with human comfort temperatures, when a room reaches a certain temperature, any additional heat or coolth is taken up in the PCM as it changes state. This energy is held by the PCM until the room becomes cooler than the PCM, which then releases its energy.

Materials that melt between 22°C and 25°C are very useful for storing winter passive solar gains. Any temperature increase over the melting point during daytime is absorbed by the PCM as it changes state. This energy stays stored until the PCM starts to solidify again as temperatures drop below the melting point at night-time. As the PCM solidifies, it releases the stored heat. PCMs work equally well in a passively cooled building if sufficient night-time cooling can drop temperatures below the PCM melting point.

Commonly used PCMs include paraffin wax, palm and coconut oil and a variety of benign salts. Several are available in Australia. PCMs have high upfront costs compared with conventional thermal mass, but can reduce costs through space and structural savings. They are a good way to install mass in existing buildings and are particularly useful in lightweight buildings. PCMs are much lighter than masonry and can be suitable in upper storeys, and can also be helpful on severely constrained sites where thermal mass would otherwise be difficult to install.

PCMs can be integrated with other building materials such as plasterboard to achieve better thermal performance. For example, the thermal capacity of a 13mm PCM plasterboard is claimed to be equivalent to 50mm of concrete. Various products are available overseas; market availability in Australia has been sporadic but may improve over time if demand increases.

• Baggs D and Mortensen N (2006). Thermal mass in building design, Environment design guide, DES 4, Australian Institute of Architects, Melbourne.
• Baggs S, Baggs D and Baggs J (1991). Australian earth-covered building, UNSW Press, Kensington, New South Wales.
• Baggs S, Baggs D and Baggs J (2009). Australian earth-covered and green roof building, 3rd edn, Interactive Publications, Wynnum, Queensland.
• Ballinger J, Prasad D and Rudder D (1992). Energy-efficient Australian housing, 2nd edn, Building Information Series, Department of Primary Industries and Energy, Canberra.
• Baverstock G and Paolino S (1986). Low energy buildings in Australia, Graphic Systems, Western Australia.
• Building Green, Thermal mass and R value: making sense of a confusing issue.
• Department of Housing and Regional Development (1995). AMCORD: a national resource document for residential development, Commonwealth of Australia, Canberra.
• Hollo N (2011). Warm house cool house: inspirational designs for low-energy housing, 2nd edn, Choice Books, NewSouth Publishing, Sydney.
• Passive and Low Energy Architecture, (PLEA) (1999). Sustaining the future: energy, ecology, architecture. In: Szokolav S (ed.), Proceedings of the 16th International PLEA Conference, Brisbane, 22–24 Sept 1999. 

Learn more

• Explore Passive heating and Passive cooling for more detail on how to make sure thermal mass works effectively in your home
• Read Orientation for how orientation and thermal mass can work together
• Refer to Shading for ways to control solar gain

Authors

Principal author: Chris Reardon 2013



Contributing authors: Caitlin McGee, Geoff Milne 2013



Updated: Andy Marlow 2020